Color Keying (Green Screen Removal)

Color keying (also called chroma keying) is a special technique that removes a specific color or color range from a picture. Essentially this technique is used to replace one background with another. Color keying is applied in many fields, such as news, motion picture, photography, video games, etc. For example, you encounter color keying while watching the forecast, when a presenter appears in front of a weather map. Usually green and blue backgrounds are used for color keying, because these colors are opposite to skin tone and the distinction is very clear. Graphics Mill provides color keying implementation removing only the green range.

You can use the GreenScreenRemoval transform or the TransformsProvider.RemoveGreenScreen() method to implement color keying. The input image can have any supported pixel format, while the output will be in the 32 or 64-bit ARGB format, where color depth depends on the number of bits per pixel in the input image. Thus if the output image format supports the alpha channel (see the Supported File Formats topic), the removed green area will be replaced with transparent.

The snippet below demonstrates how to use the RemoveGreenScreen() method to remove a green background. As the output image format is JPEG, which does not support the alpha channel, the background will be replaced with the color white:

using (var bitmap = new Bitmap(@"Images\in.jpg"))
{
    bitmap.Transforms.RemoveGreenScreen();
    bitmap.Save(@"Images\Output\out.jpg");
}

The following snippet performs the same task using the GreenScreenRemoval transform. However, here the output file format is TIFF, which supports the alpha channel, so the background will be replaced with transparent:

using (var bitmap = new Bitmap(@"Images\in.jpg"))
using (var GreenRemove = new GreenScreenRemoval())
{
    using (var newBitmap = GreenRemove.Apply(bitmap))
        newBitmap.Save(@"Images\Output\out.tif");
}

Color Keying Example

The common use case of color keying is shifting the image background with another. Graphics Mill performs this task in two steps:

1. Remove the background. You can choose between the GreenScreenRemoval class or the TransformsProvider.RemoveGreenScreen() method, but do not forget that the background should be green. The picture on the left demonstrates the original image and on the right the resulting image with the green background removed:

   

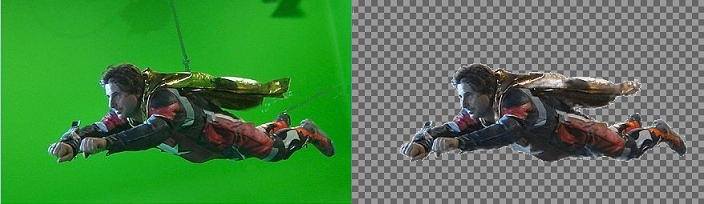
2. Combine the image with a new background using the simple overlaying method described in the Overlaying Images topic:

   

The snippet below demonstrates how to replace the image background using the RemoveGreenScreen() method:

using (var bitmap = new Bitmap(@"Images\chroma.jpg"))
using (var background = new Bitmap(@"Images\background.jpg"))
{
    //Remove the green background
    bitmap.Transforms.RemoveGreenScreen();

    //Draw the image without green-colored areas on the new background
    background.Draw(bitmap, 0, 0, CombineMode.Alpha);

    //Save the resulting image
    background.Save(@"Images\Output\out.jpg");
}

The following snippet performs the same task using the GreenScreenRemoval transform:

using (var bitmap = new Bitmap(@"Images\in.jpg"))
using (var GreenRemove = new GreenScreenRemoval())
{
    //Remove the green background
    using (var bitmapNoGreen = GreenRemove.Apply(bitmap))
    using (var background = new Bitmap(@"Images\background.jpg"))
    {
        //Draw the image without green-colored areas on the new background
        background.Draw(bitmapNoGreen, 0, 0, CombineMode.Alpha);

        //Save the resulting image
        background.Save(@"Images\Output\out.jpg");
    }
}