Affine and Projective Transformations

General Information

In mathematics, a linear transformation is a function that maps one vector space into another. Such transformations are often implemented by a matrix. A transformation is considered to be linear if it preserves vector addition and scalar multiplication. A projective transformation shows how the perceived objects change as the observer's viewpoint changes. These transformations allow the creating of perspective distortion. Affine transformations are used for scaling, skewing and rotation. Graphics Mill supports both these classes of transformations.

Both, affine and projective transformations, can be represented by the following matrix:

,

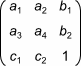where:

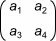is a rotation matrix. This matrix defines the type of the transformation that will be performed: scaling, rotation, and so on.

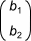is the translation vector, which specifies movement.

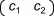is the projection vector. For affine transformations all elements of this vector are equal to 0.

Geometrical raster transformations are applied to vectors containing coordinates of a point, the x and y values of a pixel. To apply a transformation it is necessary to multiply this vector by a matrix representing the transformation:

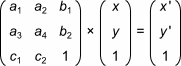
The result of this multiplication is a vector having transformed coordinates, x' and y' in the figure above.

Difference Between Projective and Affine Transformations

The sole difference between these affine and projective transformations is in the last line of the transformation matrix. For affine transformations, the first two elements of this line are zeros. This leads to the following differences in operations properties:

• Projective transformations do not preserve parallelism, length, and angle.
• Affine transformations, unlike the projective ones, preserve parallelism.

A projective transformation can be represented as the transformation of an arbitrary quadrangle (that is a system of four points) into another one. Affine transformation is the transformation of a triangle. The image below illustrates this:

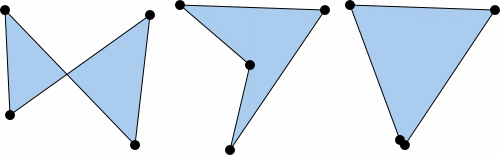
If a transformation matrix represents a non-convex quadrangle (such matrices are called singular), then the transformation cannot be performed through matrix multiplication. A quadrangle is non-convex if one of the following is true:

• the quadrangle is self-intersecting
• a vertex lies "inside" the quadrangle
• multiple vertices are situated at the same point

The image below demonstrates non-convex quadrangles:

How to Apply Projective Transformations

Generally, if you want to apply a linear transformation, you have to calculate the transformation matrix. Fortunately, Graphics Mill can do all the math for you. To apply a projective transformation in Graphics Mill perform the following steps:

1. Specify source and destination quadrangles.
2. Create the projective transformation matrix using the Matrix.CreateFromProjectivePoints(PointF[], PointF[]). Pass the previously specified point as the method arguments.
3. Create the transform using the MatrixTransform.#ctor constructor. Here the previously created matrix is the argument of the constructor.
4. Apply the transformation by calling the MatrixTransform.Apply method.

The following code applies the perspective distortion effect to a source image:

using (var bitmap = new Bitmap(@"Images\in.jpg"))
{
    System.Drawing.PointF[] source = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width, 0f)
    };

    System.Drawing.PointF[] target = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width * 0.75f, bitmap.Height - 50f),
        new System.Drawing.PointF(bitmap.Width * 0.75f, 80f)
    };

    var matrix = Matrix.CreateFromProjectivePoints(source, target);

    using (var transform = new MatrixTransform(matrix))
    {
        using (var result = transform.Apply(bitmap))
        {
            result.Save(@"Images\Output\out.jpg");
        }
    }                
}

Suppose you have the following source image:

Here is the image that will be produced by the code above:

How to Apply Affine Transformations

Affine transformations are a special case when using projective transformations: to set an affine transformation you should specify triangles. To apply an affine transformation in Graphics Mill you should perform almost the same steps as for a projective one:

1. Specify source and destination triangles.
2. Create the affine transformation matrix using the Matrix.CreateFromAffinePoints(PointF[], PointF[]). Pass the previously specified point as the method arguments.
3. Create the transform using the MatrixTransform.#ctor constructor. Here the previously created matrix is the argument of the constructor.
4. Apply the transformation by calling the MatrixTransform.Apply method.

The code below skews a source image and saves the result:

using (var bitmap = new Bitmap(@"Images\in.jpg"))
{
    System.Drawing.PointF[] source = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, 80f),
        new System.Drawing.PointF(80f, 0f)
    };

    System.Drawing.PointF[] target = {
        new System.Drawing.PointF(20, 0f),
        new System.Drawing.PointF(0f, 80f),
        new System.Drawing.PointF(80f, 0f)
    };

    var matrix = Matrix.CreateFromAffinePoints(source, target);
    
    using (var transform = new MatrixTransform(matrix))
    {
        using (var result = transform.Apply(bitmap))
        {
            result.Save(@"Images\Output\out.jpg");
        }
    }
}

Suppose you have the following source image:

Here is the image that will be produced by the code above:

See Also

Reference

• MatrixTransform Class
• Matrix Class
• Matrix.CreateFromAffinePoints(PointF[], PointF[]) Method
• Matrix.CreateFromProjectivePoints(PointF[], PointF[]) Method

Manual

• Resizing and Cropping Images
• Rotating and Flipping Images